ФІЛЄР З.Ю.
Доктор технічних, кандидат фізико-математичних наук, професор
Центральноукраїнський державний педагогічний університет
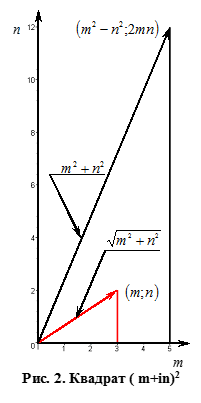
Розглянемо цілі гаусові числа (m i n – цілі числа). Для них маємо тотожність
Вона стверджує, що числа (), та створюють піфагорійську трійку (ПТ), тобто дорівнюють відповідно катетам та гіпотенузі трикутника. При будем мати єгипетську трійку 3, 4, 5; при маємо 8, 6, 10. Взяв отримаємо трійку 16, 30, 34; скоротивши, матимемо подібний трикутник зі сторонами 8, 15, 17. Легко перевірити, що він прямокутний: 82+152=172 (64+225=289).
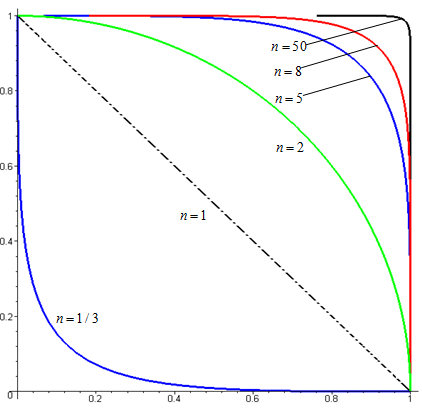
Рис. 1. На кривій x=cost, y=sint є раціональні точки; на кривих
x=cos2/nt, y=sin2/nt при таких точок немає
Як стверджується в [1, с.457] «Усі трійки взаємно простих ПТ можна отримати за формулами де і – цілі числа». Навпаки, маючи піфагорійську трійку можна знайти відповідні Для цього треба розв’язати рівняння відносно і З них маємо Так, для трійки 7, 24, 2 Очевидно,
«Натуральне гаусове число» не завжди має цілий модуль, але його квадрат завжди породжує ПТ. Це пояснює рис. 9. Число 3+4і має модуль 5, але число 3+і має модуль Його квадрат 8 + 6і має модуль 10; воно дає піфагорійську трійку 6, 8, 10.
- Інші діофантові рівняння. Використовуючи тотожність , отримаємо шо дає при цілих і цілі розв’язки рівняння При маємо рівність 22 + 112 = 53.
Рівняння дає ще формули для отримання піфагорійських трійок: , і . При будемо мати трійку 28, 96, 100, скорочуючи яку, отримаємо 7, 24, 25. Останню можно отримати за класичними формулами при
Комплексні числа стали відомі в Середньовіччя, а піфагорійські числа знали ще в давній Греції. Як вони знайшли ці формули?
- Рівняння у Великій теоремі Ферма не має натуральних розв’язків. Поділивши наотримаємо рівняння , де х та у обидва
не можуть бути раціональними при Раціональні точки мають обидві координати раціональними. Для n=2 такі точки є (3/5 і 4/5, наприклад). При отримується пряма, на якій стільки ж раціональних точок, скільки їх на відрізку . При отримаємо рівняння яке має раціональні розв’язки (наприклад, ).
З рівняння (1) випливає . Розкладаючи в ряд, отримаємо
При ряд збіжний при натуральних n. При раціональних х всі члени цього ряду є раціональними, але його сума за теоремою Ферма при n>2 завжди ірраціональна. Поблизу точки 0 й великому з високою точністю У зв’язку із симетрією рівняння (1) відносно х і у, теж буде при Крива близька до контуру квадрата (Рис. 1 при
- Зображення нескінчених множин. У 80-х роках автор здогадався зображати трансфінітні числа Кантора на кінцевих відрізках числової прямої. У 1987 р. їм була зроблена на цю тему доповідь на Міжнародному конгресі з логіки, методології і філософії науки. У [1] ця ідея була повторена. При цьому таке число w було межею геометричної прогресії, наприклад, із знаменником q=1/2. Послідовність 1. 2, 3., … до , укладається на відрізку [1, L), L=1/(1-q). Ця ідея реалізується і числову вісь, площину і простір за формулою x’=x/|x|(1-q|x|)/(1-q). Зокрема, площина відобразиться в круг радіуса R=1/(1-q). При цьому нескінчені лінії будуть зображені в цьому крузі; їх точки будуть мати ті самі аргументи. Нескінченно віддалені точки перейдуть в точки граничного кола.
Цей підхід може бути використаний для встановлення стійкості лінійних диференціальних рівнянь. Рівняння n-го порядку має характеристичний поліном f(λ)=a0+a1λ+a2λ2+…+an-1λn-1+anλn. Асимптотична стійкість буде, якщо годограф функції f(iω)=a0-a2ω2+…+i(a1λ-a3λ3+…) буде робити поворот навколо точки О проти годинникової стрілки на кут nπ/2. Цей алгоритм легко реалізувати з допомогою пакета Maple, в якому є програма для побудови комплексних функцій. В ньому будується лінія за формулою
W=f(it)/|f(it)|(1-q|f(it)|)/(1-q), 0<q<1, 0≤t<ω. Цей метод можна застосовувати і для диференціальних рівнянь з запізненням. Так для рівняння
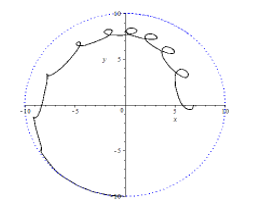
Рис. 3. Годограф рівняння із запізненням на 19
Тепер будуємо криву – годограф з характеристичним є квазіполіном f(z)=9+2e– I9z +17z+5z2+3z3 на фінітній площині (Рис. 3).
Список використаних джерел
1. Філєр З.Ю. Проблеми нескінченності у математиці, фізиці та філософії// Комбінаторні конфігурації та їх застосування. 5-й Міжвузівський науково-практичний семінар. – Кіровоград: КК-ТК, 2008. – С. 84 – 95.
